문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
입출력 예시
입력
4 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
2 2 3 4
3 4 3 4
1 1 4 4
출력
27
6
64
풀이
'use strict';
const fs = require('fs');
// 백준 제출 할 때 주석 제거
// const readFileSyncAddress = '/dev/stdin';
// VSC 테스트 할 때 주석 제거
const readFileSyncAddress = 'input.txt';
const input = fs.readFileSync(readFileSyncAddress).toString().trim().split('\n');
const condition = input.shift().split(' ').map(Number);
const n = condition[0];
const m = condition[1];
function solution(input, n, m) {
const numberList = [];
const dp = Array.from({ length: n + 1 }, () => Array(n + 1).fill(0));
for (let i = 0; i < n; i++) {
const temp = input.shift().split(' ').map(Number);
numberList.push(temp);
}
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + numberList[i - 1][j - 1];
}
}
for (let i = 0; i < m; i++) {
const loc = input[i].split(' ').map(Number);
const x1 = loc[0];
const y1 = loc[1];
const x2 = loc[2];
const y2 = loc[3];
console.log(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]);
}
}
solution(input, n, m);
2차원 누적합을 계산할 때 꼭 고려해야 할 한 가지
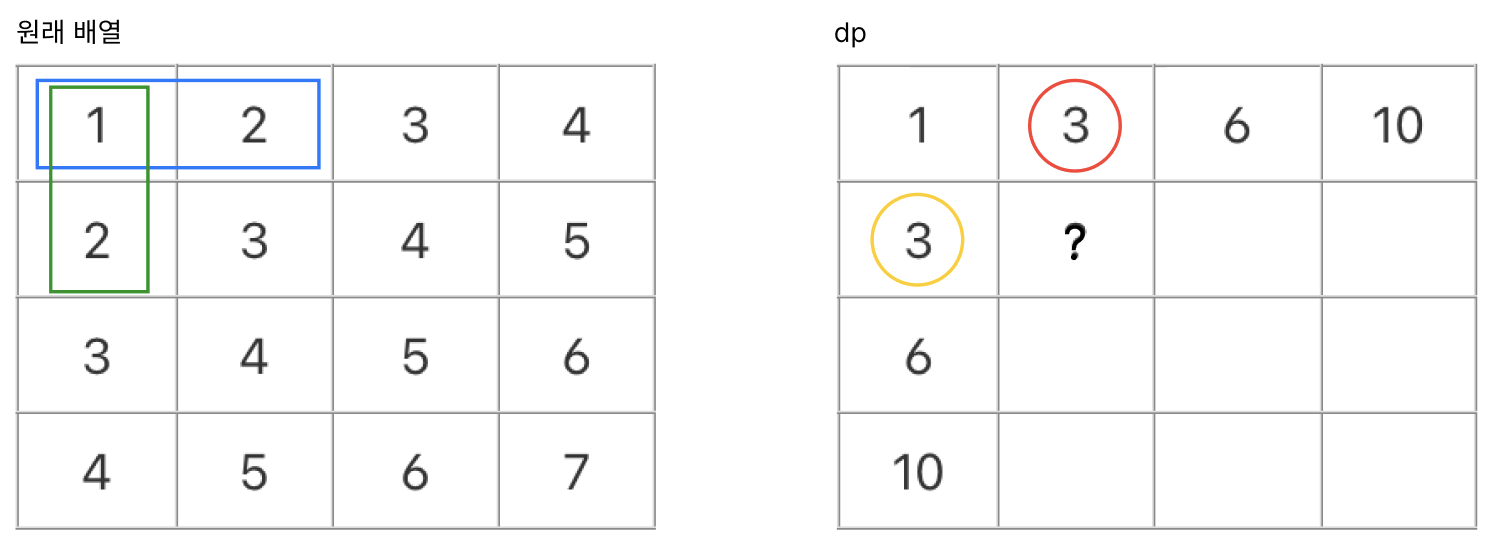
위의 그림처럼, 왼쪽은 원본 배열이고 오른쪽은 누적합(dp 배열)입니다.
이제 오른쪽 dp 배열에서 빨간색 원 안의 숫자 3이 어떻게 나왔는지 생각해보겠습니다.
이 값은 원본 배열에서 파란색 네모(1, 2)의 합입니다. 즉, 1 + 2 = 3.
마찬가지로, 노란색 원 안의 3은 초록색 네모(1, 2)의 합이죠.
그렇다면, ? 위치에 들어갈 값은 어떻게 계산해야 할까요?
처음 떠오를 수 있는 방법
상단(3)과 좌측(3)의 값을 더해주면 6이 되니,
여기에 자기 자신(3)을 더해주면 9?
NO!
이렇게 단순히 상단과 좌측을 더하면 왼쪽 위 값인 1이 두 번 더해지게 됩니다.
겹치는 영역은 빼줘야 한다
dp 배열은 누적합이기 때문에, 상단과 좌측을 더하면 원래 한 번만 포함되어야 할 1이 중복됩니다.
따라서 중복된 1을 한 번 빼줘야 정확한 누적합이 나옵니다.
공식으로 표현하면 이렇게 됩니다.
dp[y][x] = dp[y-1][x] + dp[y][x-1] - dp[y-1][x-1] + original[y][x]
2차원 누적합(dp)을 이용해 부분 합 구하기
2차원 배열에서 특정 영역의 합을 빠르게 구하고 싶을 때, DP(Prefix Sum) 배열을 만들어두면 O(1) 시간에 계산할 수 있습니다!
예제로 아래 그림을 함께 보겠습니다.
단순히 뺀다고 해결될까?

오른쪽의 dp 배열은, 왼쪽 원본 배열의 누적합을 나타냅니다.
우리가 알고 싶은 건, 빨간색 네모 영역(부분 배열)의 합입니다.
이때, 가장 쉽게 생각할 수 있는 방법은
dp[x2][y2] - dp[x1][y1] 하면 되지 않을까?
하지만 실제로 그렇게 하면 정확한 값이 나오지 않습니다.
왜냐하면, 이 계산 과정에서 겹치거나 빠지는 부분이 생기기 때문입니다.
누적합을 뺄 때 주의해야 할 점

이제 왜 단순히 빼는 것이 안 되는지 시각적으로 살펴보겠습니다.
dp[x2][y2]-dp[x1][y1]을 하게 되면 파란색 네모 영역에서 초록색 네모 영역을 제외하게 되는데 한눈에 봐도 잘못된 계산이라는 것을 알 수 있습니다.

- 보라색 원: 파란 네모 영역의 누적합
→ dp[x1-1][y2] - 주황색 원: 초록 네모 영역의 누적합
→ dp[x2][y1-1]
파란 네모 + 초록 네모를 빼면 "겹치는 영역"이 두 번 빠짐
파란 네모와 초록 네모가 겹치는 영역이 한 번씩 두 번 빠지게 됩니다.
이 겹치는 영역은 노란색 원에 해당합니다.
결국 노란색 원은 한 번만 빠져야 하므로, 다시 한 번 더해줘야 합니다.
→ dp[x1-1][y1-1]
공식으로 표현하면 이렇게 됩니다.
dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]
'알고리즘' 카테고리의 다른 글
| [ 백준 ] 1260 DFS와 BFS - JavaScript (0) | 2025.03.31 |
|---|---|
| [ 프로그래머스 ] 단속카메라 - JavaScript (0) | 2025.03.31 |
| [ 백준 ] 12933 오리 - JavaScript (0) | 2025.03.29 |
| [ 백준 ] 1541 잃어버린 괄호 - JavaScript (0) | 2025.03.29 |
| [ 백준 ] 10799 쇠막대기 - JavaScript (1) | 2025.01.07 |